Many of you ML enthusiasts out there might have used boosting algorithms to get the best predictions (most of the time) on your data. In this blog post, I want to demystify how these algorithms work and how are they different from others. But why would anyone want to do the tough job of looking under the hood to understand the inner working? This post is for all the curious minds out there who want to learn and innovate new techniques to tackle unprecedented problems. Let’s get started!

Table of Content

1. Supervised Machine Learning
2. Gradient Descent Algorithm
3. Optimization in function space
4. Gradient Boosting Algorithm
5. XGBoost

Supervised Machine Learning

To solve any supervised Machine Learning problem, given the dataset $\{(x_i, y_i)\}_{i=1,\ldots,n}$ where $x$ are the features and $y$ is the target, we try to restore the function $y = f(x)$ by approximately estimating $\hat{f}(x)$ while measuring how good the mapping is using a loss function $L(y,f)$ and then take average over all the dataset points to get the final cost, i.e., $\hat{f}(x) = \underset{f(x)}{\arg\min}\mathbb{E}_{x,y}[L(y,f(x))]$

The only problem that remains is to find the $\hat{f}(x)$. Since there are infinite possibilities/combinations to create a function, the functional space is infinite-dimensional. Why is it infinite? You can create a function which is a simple linear combination of your features, or you can go crazy and create a function which contains polynomial, trigonometric,exponential, logarithmic terms, etc. and is piece-wise continuous and what not. Hence, to find a function we need to limit our search space by restricting our function to a specific structure, $f(x,\theta), \theta \in \mathbb{R}^n$. Remember your linear regression equation? There we only consider linear combination of features i.e. $\hat{f}(x) = \theta^Tx$, we are limiting the search space to find parameters $\theta$, this is similar to that. The structure helps us limit our craziness and give the function a sense of belongingness to a family. The optimization problem has now become, $\hat{\theta} = \underset{\theta}{\arg\min} \mathbb {E}_{x,y}[L(y,f(x,\theta))]$, so we only need to search over $\theta$.

Gradient Descent Algorithm

We can find this by updating $\theta$ in an iterative fashion using our favorite gradient descent algorithm and come up with our estimate $\hat{\theta}$ after $T$ iterations, $\hat{\theta} = \sum_{i = 1}^T \hat{\theta_i}$. To start we initialize $\hat{\theta} = \hat{\theta_0}$ and at each iteration we calculate the gradient of loss function, i.e. $-\left[\frac{\partial L(y, f(x, \theta))}{\partial \theta}\right]_{\theta = \hat{\theta} }$. The gradient tells us in which direction we should move or update our parameter to minimize the loss, let’s call this gradient/update $\hat{\theta_t}$ for the $t^{th}$ step. We add this $\hat{\theta_t}$ to our current estimate to get the new estimate, $\hat{\theta} \leftarrow \hat{\theta} + \hat{\theta_t} = \sum_{i = 0}^t \hat{\theta_i}$ . We repeat this till convergence, when the gradient of the loss function is close to 0. Finally, we have the $\hat{f}(x) = f(x, \hat{\theta})$.

Optimization in function space

Let’s take a pause and understand why we had to go through all this. Here, in the gradient descent algorithm we did an iterative search over the parameters. Why can’t we search in the same way over functions? We can start with a randomly guessed function and keep adding new functions to get better estimate like we did with parameters. We will start with our initial estimate $\hat{f}_0$ and then reach to our final function after $T$ iterations, $\hat{f}(x) = \sum_{i=0}^T\hat{f_i}(x)$. Same as earlier, we will restrict our functions to a family, $\hat{f}(x) = g(x,\theta)$. We will also search for an optimal coefficient $\rho$ for each function we want to add. In $t^{th}$ iteration, the optimization problem becomes,

$\hat{f}(x) = \sum_{i = 0}^{t-1} \hat{f_i}(x)$

$(\rho_t,\theta_t) = \underset{\rho,\theta}{\arg\min}\mathbb {E}_{x,y}[L(y,\hat{f}(x) + \rho \cdot g(x, \theta))]$

$\hat{f_t}(x) = \rho_t \cdot g(x, \theta_t)$

Now, we will try to solve this using gradient descent. But how? We can calculate gradient of loss with respect to the function instead of a parameter. Suppose we are using squared error $L = (y-f)^2$, the gradient of the loss w.r.t. $f$ will be $[\frac{\partial L(y, f)}{\partial f}]_{f=\hat{f}} = -2*(y-\hat{f})$, which is the $residual$. So the new function that needs to be added to our previous estimate should be equal to the $residual$. This makes sense, right? We are adding a new function to the previous estimate to correct wherever it had made errors. So now in $t^{th}$ iteration, the optimization problem becomes,

$\hat{f}(x) = \sum_{i = 0}^{t-1}\hat{f_i}(x)$, $r_{it} = -\left[\frac{\partial L(y_i, f(x_i))}{\partial f(x_i)}\right]_{f(x)=\hat{f}(x)}, \quad {for}\ i=1,\ldots,n$

$\theta_t = \underset{\theta}{\arg\min}\sum_{i = 1}^{n} (r_{it} - g(x_i, \theta))^2,$

$\rho_t = \underset{\rho}{\arg\min}\sum_{i = 1}^{n} L(y_i, \hat{f}(x_i) + \rho \cdot g(x_i, \theta_t))$

Gradient Boosting Algorithm

We can solve these above equations to find $\hat{f}$ in an iterative manner as shown below:

1. Initialize the function estimate with a constant value$\hat{f}(x) = \hat{f}_0, \hat{f}_0 = \gamma, \gamma \in \mathbb{R}, \hat{f}_0 = \underset{\gamma}{\arg\min}\sum_{i = 1}^{n} L(y_i, \gamma)$

2. For each iteration $t = 1, \dots, T$:

   i. Calculate pseudo-residuals $r_t$, $r_{it} = -\left[\frac{\partial L(y_i, f(x_i))}{\partial f(x_i)}\right]_{f(x)=\hat{f}(x)}, \quad{for }\ i=1,\ldots,n$

   ii. Add a new function $g_t(x)$ (it can be any model, but here we are using decision trees) as regression on pseudo-residuals $\{ (x_i, r_{it})\}_{i=1, \ldots,n}$

   iii. Find optimal coefficient $\large \rho_t$ at $g_t(x)$ regarding initial loss function $\rho_t = \underset{\rho}{\arg\min}\sum_{i = 1}^{n} L(y_i, \hat{f}(x_i) + \rho \cdot g_t(x_i, \theta))$

   iv. Update current approximation $\hat{f}(x)$ where $\hat{f_t}(x) = \rho_t \cdot g_t(x)$

   $\hat{f}(x)\leftarrow\hat{f}(x)+\hat{f_t}(x) = \sum_{i = 0}^{t}\hat{f_i}(x)$

3. The final GBM model will be sum of the initial constant and all the subsequent function updates $\hat{f}(x) = \sum_{i = 0}^T\hat{f_i}(x)$

This is how the Gradient Boosting Machines algorithm works.

XGBoost

XGBoost is a scalable machine learning system for tree boosting. The system is available as an open source package. The impact of the system has been widely recognized in a number of machine learning and data mining challenges. It became well known in the ML competition circles after its use in the winning solution of the Higgs Machine Learning Challenge. Many of the winning solutions in Kaggle competitions have used XGBoost to train models. Its popularity and success is an outcome of the following innovations:

1. Scalable end-to-end tree boosting
2. Weighted quantile sketch to propose efficient candidate split points
3. Sparsity-aware algorithm that handles sparse data including missing values
4. Effective cache-aware block structures for out of the core computing

The derivation follows from the same idea of gradient boosting as we saw earlier.

It uses K additive trees to create the ensemble model,

$\hat{y} = \hat{f}(x) = \sum_{i = 0}^K\hat{f_i}(x)$, $\hat{f_i}(x) \in F$

where $ F = {f(x) = w_{q(x)}}(q: \mathbb{R}^{m} \rightarrow T, w \in \mathbb{R}^{T})$

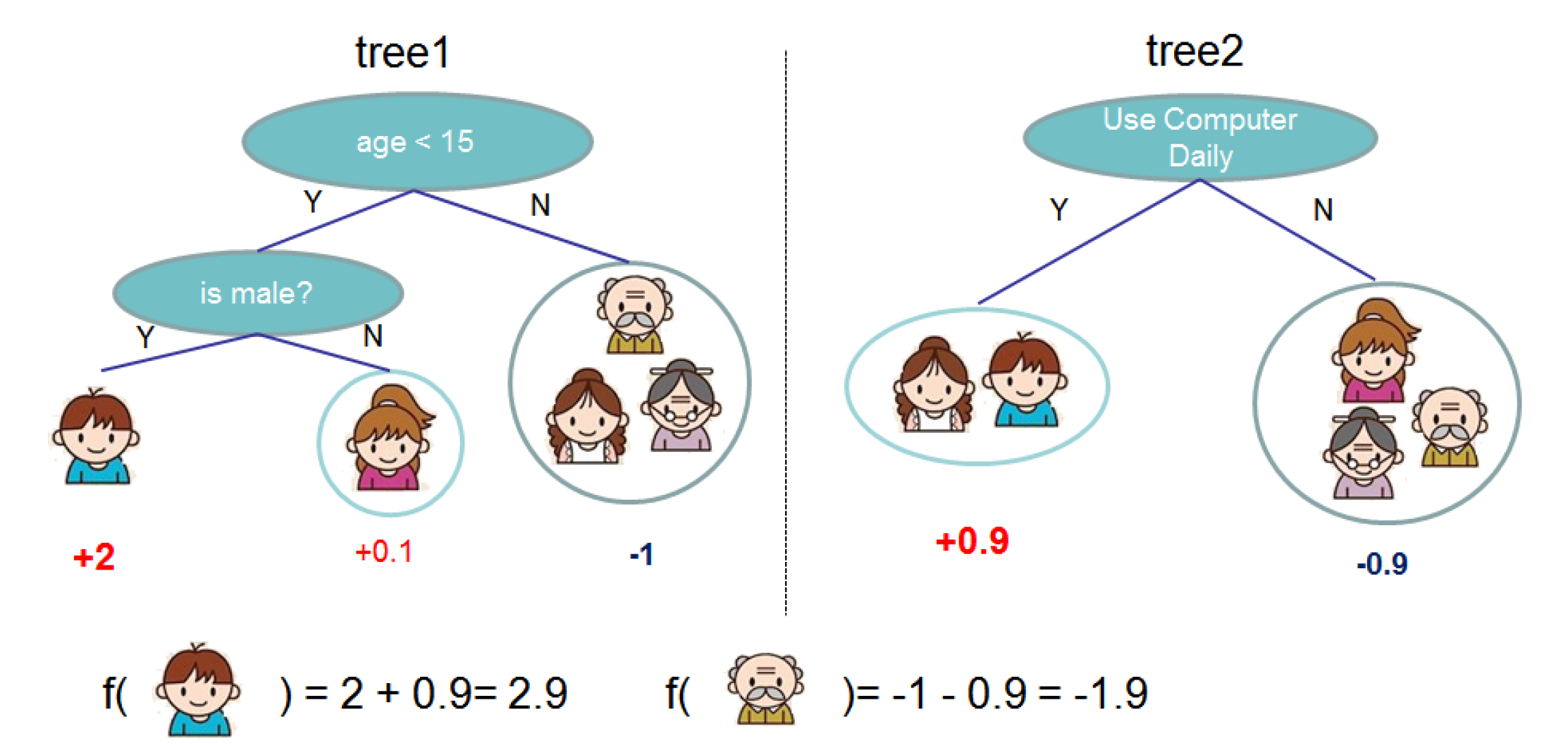
$q$ represents the structure of the tree that maps an input to the corresponding leaf index at which it ends up being. $T$ is the number of leaves in the tree. Each regression tree contains a continuous score on each of its leaf. $w_i$ represents the score on i-th leaf. For a given example, we will use the decision rules in the trees (given by $q$) to classify it into the leaves and calculate the final prediction by summing up the score in the corresponding leaves (given by $w$) as shown in the image below.

To learn the set of functions used in the model, we minimize the following regularized objective.

$\mathcal{L}(\phi) = \sum_{i} l(\hat{y}_i,y_i) + \sum_{k} \Omega(f_{k})$

where $\Omega(f_{k}) = \gamma T + \frac{1}{2}\lambda ||w||^{2}$

Here $l$ is a differentiable convex loss function that measures the difference between the prediction $y_i$ and the target $y_i$.The second term penalizes the complexity of the model (i.e., the regression tree functions). The additional regularization term helps to smooth the final learnt weights to avoid over-fitting. Trees with more depth have too many leaf nodes and can overfit on the training data, with very few examples ending up in each leaf node. Hence to reduce the depth and overfitting we use a penalty for number of leaf nodes. When the regularization parameter is set to zero, the objective falls back to the traditional gradient tree boosting.

For the t-th iteration we will need to add $f_t$ to minimize the following objective function,

$\mathcal{L}^{(t)} = \sum_{i} l(\hat{y}_i^{t-1}+f_{t}(x_{i}),y_i) + \sum_{t} \Omega(f_{t})$

Using Taylor series expansion we can do second-order approximation of our objective function. A Taylor series is a series expansion of a function about a point. A one-dimensional Taylor series is an expansion of a real function f(x) about a point x=a, is given by

$f(x) = f(a) + f^{\prime}(a)(x-a)+ \frac{f^{\prime\prime}(a)}{2!} (x-a)^2 + …+ \frac{f^{n}(a)}{n!} (x-a)^n + … $,

Applying second order approximation to our function and ignoring higher order terms,

$\mathcal{L}^{(t)} = \sum_{i}^n [l(\hat{y}_i^{t-1}, y_i) + g_i f_{t}(x_{i}) + \frac{1}{2}h_if_{i}^2(x_{i})] +\Omega(f_{t})$

For comparison with Taylor Series, we have $(\hat{y}_i^{t-1}, y_i)$ as x and $f_{t}(x_{i})$ as x-a, and $g_{i} = \partial_{\hat{y}^{t-1}}l(\hat{y}_i^{t-1}, y_i)$ and $h_{i} = \partial_{\hat{y}^{t-1}}^2l(\hat{y}_i^{t-1}, y_i)$, which is the first and second derivative respectively. This approximation helps in getting a closed form optimal solution for $w$.

We can remove the constant terms to simplify the objective function ,

$\mathcal{L}^{(t)} = \sum_{i}^n [g_i f_{t}(x_{i}) + \frac{1}{2}h_if_{i}^2(x_{i})] +\Omega(f_{t})$

Let $I_{j} = \{i|q(x_{i})=j\}$ be the instance set of leaf j, i.e. set of all the input data points that ended up in j-th leaf node. So, for a given tree, if our input data point ends up in some j-th leaf node after going through all the decisions, we are going to put that data point in our set $I_{j}$. We can rewrite the objective function as follows,

$\mathcal{L}^{(t)} = \sum_{i}^n [g_i f_{t}(x_{i}) + \frac{1}{2}h_if_{t}^2(x_{i})] + \gamma T + \frac{1}{2}\lambda||w||^{2}$

$= \sum_{j=1}^T[(\sum_{i \in I_{j}}g_{i})w_{j} + \frac{1}{2}(\sum_{i \in I_{j}}h_i + \lambda)w_{j}^2] +\gamma T$

For a fixed tree structure $q(x)$, we can compute the optimal weight $w_{j}^{*}$ of leaf j by differentiating the above equation with respect to w and equating to 0,

$w_{j}^{*} = -\frac{\sum_{i \in I_{j}}g_{i}}{\sum_{i \in I_{j}}h_{i}+\lambda}$,

Here, for now we are assuming that we have a tree structure $q$ for which we have found the corresponding optimal weights at each leaf node. If you observe the above equation of $w_{j}^{*}$ you will notice that we don’t have the leaf nodes yet, i.e. $I_{j}$ haven’t been calculated so far. What we currently have is, given any tree structure we can find what the optimal leaf node weights should be. Our next steps are all about finding the optimal tree structure that minimizes the loss and then we are done finding our tree.

We now calculate the corresponding optimal value for given tree structure $q$ by replacing $w_{j}^{*}$ in the above equation (calculation is shown in the image below),

$\mathcal{L}^{(t)}(q) = -\frac{1}{2}\sum_{j=1}^{T}\frac{(\sum_{i \in I_{j}}g_{i})^2}{\sum_{i \in I_{j}}h_{i}+\lambda} +\gamma T$

We have the optimal weight for each of the leaf nodes, we now need to search for the optimal tree structure. The above equation can be used to measure the quality of a tree structure $q$. The score is like the impurity score for evaluating the trees, except that it is derived for a wider range of objective functions.

Normally it is impossible to enumerate all the possible tree structures q. A greedy algorithm that starts from a single leaf and iteratively adds branches to the tree is used instead. Assume that $I_{L}$ and $I_{R}$ are the instance sets of left and right nodes after the split. Letting $I = I_{L} \cup I_{R}$, then the loss reduction after the split is given by,

$\mathcal{L}_{split} = \frac{1}{2}[\frac{(\sum_{i \in I_{L}}g_{i})^2}{\sum_{i \in I_{L}}h_{i}+\lambda} + \frac{(\sum_{i \in I_{R}}g_{i})^2}{\sum_{i \in I_{R}}h_{i}+\lambda} - \frac{(\sum_{i \in I}g_{i})^2}{\sum_{i \in I}h_{i}+\lambda}] -\gamma (T+1 - T)$

$= \frac{1}{2}[\frac{(\sum_{i \in I_{L}}g_{i})^2}{\sum_{i \in I_{L}}h_{i}+\lambda} + \frac{(\sum_{i \in I_{R}}g_{i})^2}{\sum_{i \in I_{R}}h_{i}+\lambda} - \frac{(\sum_{i \in I}g_{i})^2}{\sum_{i \in I}h_{i}+\lambda}] -\gamma$,

i.e. total loss after split - total loss before split.

This score can be used to evaluate the split candidates similar to gini index or entropy.

XGBoost uses approximate algorithm to decide the candidate split points using Weighted Quantile Sketch, instead of greedily searching over all the split points. As it is impossible to do it efficiently when data doesn’t fit entire memory.

Besides regularisation, shrinkage $\eta$ is used to scale newly added weights after each step of tree boosting, similar to learning rate in stochastic optimization. This reduces the influences of each tree and leaves space for improvement for future trees, which helps in creating smoother boundaries and better generalization. Also similar to Random Forest, column subsampling is also used which reduces overfitting (more than traditional row sampling) and also speeds up computation.

In addition to this, algorithm is aware of the sparsity pattern in the data. A default direction is chosen in each tree node when a value is missing in the sparse matrix and the instance is classified into the default direction. The optimal default direction is learnt from the data (not covered in this post).

Hope this helps you to understand the inner workings of XGBoost algorithm and gives you a head start in reading the paper. I would urge the readers to go read the entire paper for more details that I haven’t included in this post. Please find the link to the paper in reference section below.

References:

https://mlcourse.ai/articles/topic10-boosting/

XGBoost Paper Images in this post are snipped from this paper

---

• Next Post →